One of our servers at work has a power supply that is cooled with two small, loud fans—loud enough that the noise is annoying for the occupants of the office suite shared by the server. What I’d like to do is muffle the sound by enclosing the rear of the server (or potentially just the power supply exhaust) with an actively vented box. Since the fan on the box will be larger, it should be able to move the same amount of air with less noise.
But messing around with the way servers cool themselves is tricky, and since the server isn’t easily accessible, I’d like to be able to monitor what’s going on until I confirm my setup is able to keep the server cool.
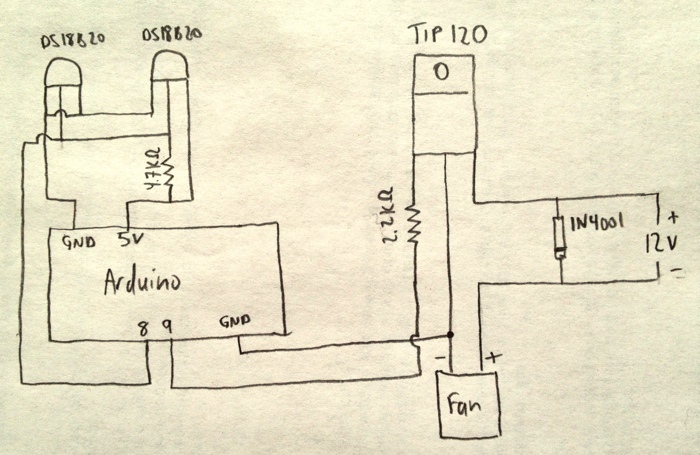
I’ve built quite a few temperature monitoring circuits, but in this project I’ll need to be able to control the speed of the vent fan based on the temperature differential inside and outside the box. This is complicated because the Arduino runs on 5 volts and the fan I’m starting with requires 12 volts. I’ll use a Darlington transistor, which can be triggered using the low power available from an Arduino pin, but which can carry the voltage and current of the fan. For higher voltages and currents, or for controlling devices that run on alternating current, I’d need to use some form of relay.
To measure the temperature differential between the inside and outside of the enclosure, I’m using two DS18B20 temperature sensors, each wired to the end of a length of Cat5e cable (and wrapped in silicone “Rescue Tape” as an experiment). The transistor is a TIP120, and a 1N4001 diode across the positive and negative leads of the fan protect it from reverse voltages when the fan is turned off but is still spinning. A 2.2KΩ resistor protects the trigger pin on the Arduino.
Here’s the diagram:
The Arduino is currently programmed to turn the fan on full speed when the temperature from the sensor inside the box is more than six degrees higher than the temperature outside the box. The fan runs at half speed until there’s less than a two degree differential, at which point the fan shuts off. These targets are hard-coded in the software, but it wouldn’t be too difficult to change the code to read from the serial buffer so that the thresholds could be changed while it’s running.
Here’s the setup code:
#include <OneWire.h>
#include <DallasTemperature.h>
#define ONE_WIRE_BUS 8
#define TEMPERATURE_PRECISION 12
#define fanPin 9
OneWire oneWire(ONE_WIRE_BUS);
DallasTemperature sensors(&oneWire);
DeviceAddress thermOne = { 0x28,0x7A,0xBA,0x0A,0x02,0x00,0x00,0xD1 };
DeviceAddress thermTwo = { 0x28,0x8B,0xFD,0x0A,0x02,0x00,0x00,0x96 };
void setup() {
Serial.begin(9600);
pinMode(fanPin, OUTPUT);
digitalWrite(fanPin, LOW);
sensors.begin();
sensors.setResolution(thermOne, TEMPERATURE_PRECISION);
sensors.setResolution(thermTwo, TEMPERATURE_PRECISION);
}
void printTemperature(DeviceAddress deviceAddress) {
float tempC = sensors.getTempC(deviceAddress);
Serial.print(DallasTemperature::toFahrenheit(tempC));
}
And the loop that does the real work:
void loop() {
sensors.requestTemperatures();
printTemperature(thermOne);
Serial.print(",");
printTemperature(thermTwo);
Serial.print(",");
float thermOneF = DallasTemperature::toFahrenheit(sensors.getTempC(thermOne));
float thermTwoF = DallasTemperature::toFahrenheit(sensors.getTempC(thermTwo));
float diff = thermOneF - thermTwoF;
Serial.print(diff);
Serial.print(",");
if ((diff) > 6.0) {
Serial.println("high");
digitalWrite(fanPin, HIGH);
} else if (diff > 2.0) {
Serial.println("med");
analogWrite(fanPin, 127);
} else {
Serial.println("off");
digitalWrite(fanPin, LOW);
}
delay(10000);
}
When I’m turning the fan off or on, I’m using digitalWrite, but when running the fan at half-speed, because I’m using a pulse-width-modulation (PWM) digital pin, I can set the pin to a value between 0 (off all the time) and 255 (on all the time) and cause the fan to run at whatever speed I want. I’m also dumping the temperatures and fan speed setting to the serial port so I can read those values later and evaluate how well the setup is working.
Last week I got permission to install a simple weather station where I work at ABR. The Fairbanks office is located on Goldstream Road, just past the intersection of Murphy Dome Road, across the street from the Peat Ponds. It’s on the uphill side of a south facing slope, and is about half a mile from Goldstream Creek. More importantly for me, I can find out what the temperature is at work when I’m dressing for riding my bike or skiing.
We ran three Cat5e cables from the computer room, outside and under a footpath, then down the hill from the Main building. The cables end up in a mixed spruce-birch forest, and the sensors will be about six feet off the ground in one of those cylindrical “white plate” style enclosures.
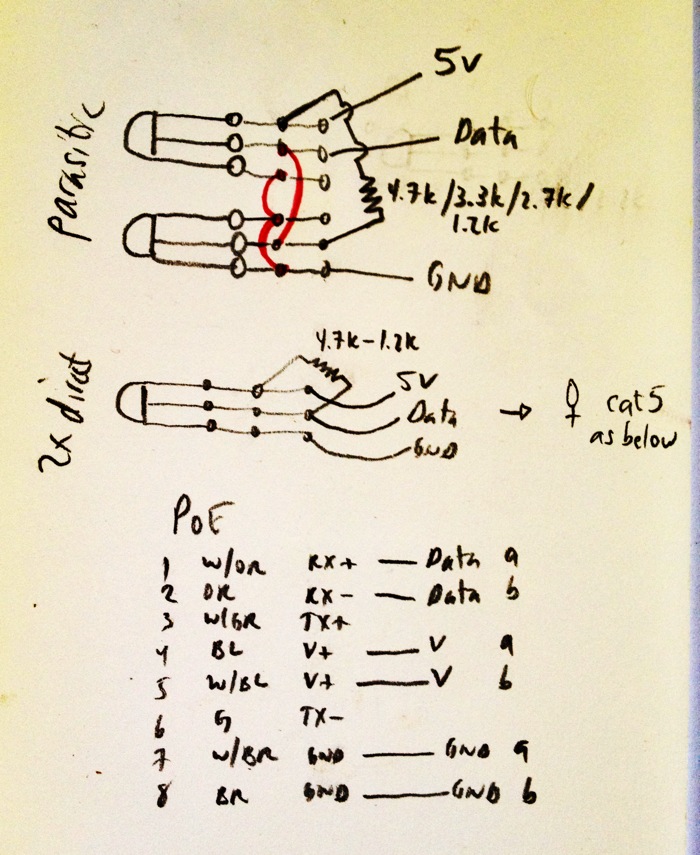
I’m using a pair of DS18B20 temperature sensors, which have a 0.5°C accuracy across their range, and will work down to -67°F. The data is retrieved using the One-Wire protocol, which is well supported by Arduino. I built a prototype of the sensor before soldering it down on a board because longer distances can require a smaller pull-down resistor than the 4.7KΩ typically used between the voltage and data lines. I also wanted to experiment with whether I could run two using parasitic power, or would need two data lines. As it turned out, 4.7KΩ worked, as did parastic power mode.
The schematic is below, including the wires I used in the Cat5e cable. I followed the PoE standard, even though I could really have used whatever wires I wanted.
I also used a contributed library called DallasTemperature which abstracts most of the work of using OneWire and converting the values into meaningful temperatures. Here's the setup code:
#include <OneWire.h>
#include <DallasTemperature.h>
#define ONE_WIRE_BUS 8
#define TEMPERATURE_PRECISION 9
OneWire oneWire(ONE_WIRE_BUS);
DallasTemperature sensors(&oneWire);
// Use a testing program to find your addresses:
DeviceAddress thermOne = {
0x28, 0xBC, 0x29, 0xE3, 0x02, 0x00, 0x00, 0xE1 };
DeviceAddress thermTwo = {
0x28, 0xCF, 0x97, 0xE3, 0x02, 0x00, 0x00, 0xCD };
void setup(void) {
Serial.begin(9600);
sensors.begin();
sensors.setResolution(thermOne, TEMPERATURE_PRECISION);
sensors.setResolution(thermTwo, TEMPERATURE_PRECISION);
}
And the part that does the work:
void printTemperature(DeviceAddress deviceAddress) {
float tempC = sensors.getTempC(deviceAddress);
Serial.print(DallasTemperature::toFahrenheit(tempC));
}
void loop(void) {
sensors.requestTemperatures();
printTemperature(thermOne);
Serial.print(",");
printTemperature(thermTwo);
Serial.println();
delay(1000);
}
Here’s the schematic. The top form shows two sensors in parasitic power mode (where you only need a single data line, power and ground), and the bottom form shows how you’d wire a single sensor. If I had trouble with getting reliable data from the sensors in parasitic mode, or with a 4.7KΩ resistor, I would have dropped the resistor to 3.3KΩ or 2.2KΩ. The next thing I would have tried would be running power and ground to both sensors separately (coming from wires 4 and 7 in the cable), and used wire 1 and wire 2 for the data lines to each sensor. As it turned out, I’m only using three of the eight wires in the cable.
Update 2012-10-15: I moved the resistor from the sensor board (you can see it in the photograph at the top of the page) to the Arduino end of the cable inside ABR, and the data is still flowing. I was a little concerned that the resistor might be adding a small amount of heat to the enclosure, and putting it at the Arduino side prevents that possibility.
Update 2012-10-19: Today I added a third DS18B20 in parasitic mode and I’m getting data from all three sensors. I would guess the total cable run is around 100 feet from the Arduino to the sensors. So: 100 feet of Cat 5e, three sensors in parasitic mode, with a 4.7KΩ pull-down resistor between power and data on the Arduino side of the cable.

Boil
Over the past month and a half I’ve brewed four beers, starting with Piper’s Irish-American Ale , and culminating with Mr. Silly IPA which is in the middle of the mash right now. We’re less than a week from when we normally get the first snowfall that lasts until spring, so this will likely be the end of my 2012 brewing effort.
My normal process is to make a yeast starter from a Wyeast smack-pack or White Labs tube, pitch that into the first batch, and a week later siphon the chilled wort of the second batch onto the yeast cake from the first.
I didn’t have time to make a starter for Piper’s, so I just smacked the pack (Wyeast 1084, Irish Ale) on brew day and assumed there’d be enough healthy yeast to make quick work of the 1.049 wort. After two days of no visible activity, I began to worry that the yeast in the pack had been killed at some point before I bought it. Finally on day three, something finally started to happen and the beer has since fermented successfully.
The second batch was a 1.077 old ale I poured into my Old Alexi solera ale keg (recipe is here). It kicked off almost immediately and was probably 90% fermented within 24 hours due to the thick, healthy yeast from fermenting Piper’s.
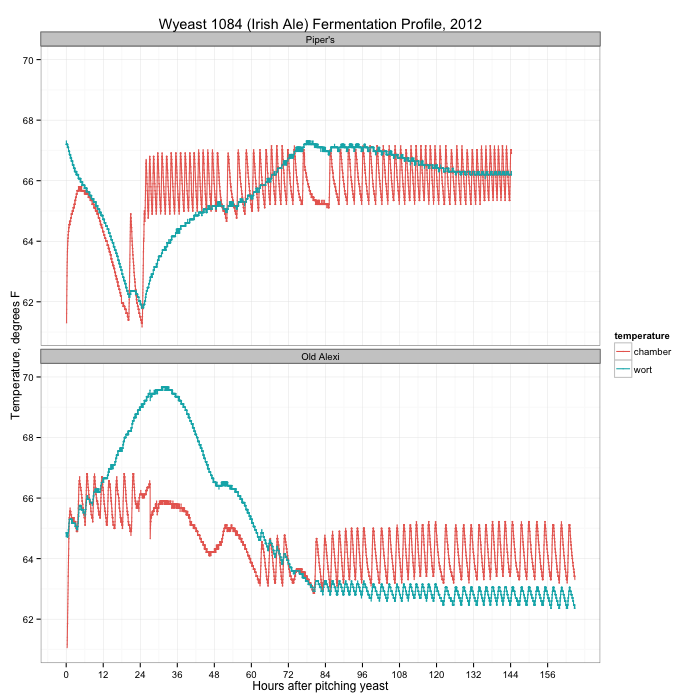
During both fermentations I kept track of the temperatures in the fermentation chamber (a fridge with heater on a temperature controller) and in the wort using my Arduino data logger. A graph of the two fermentations is below:
You can see the activity of the temperature controller on the temperature in the chamber (the orange line), clicking the heater on and off within 4 degrees of the set temperature. For Piper’s (the top plot) I started with the chamber at 64°F, but almost immediately bumped it up to 66°F when the wort temperature crashed. After 24 hours, something finally started happening in the wort, with a peak temperature (and fermentation) on day three. When I transferred the wort from primary to secondary on day seven, there was still active fermentation.
Compare this with the second beer. The wort started at 65°F, and immediately took off, peaking a little over 24 hours later. By day three, fermentation was over. I dropped the fermentation chamber temperature from 66°F to 64°F after the first day.
What did I learn? First: always make a yeast starter. It’s no fun waiting several days for fermentation to finally take off, and during that lull the wort is vulnerable to other infections that could damage the flavor. Second: don’t panic, especially with a yeast that has a reputation of starting slowly like Wyeast 1084. It usually works out in the end. More often than not, the Papazian “relax, enjoy a homebrew” mantra really is the way to approach brewing.
I used a starter for last week’s batch (Taiga Dog AK Mild, White Labs WLP007, Dry English Ale) and it was visibly fermenting within a day and a half. Mr. Silly will undoubtedly have a similar fermentation temperature curve like Old Alexi above after I transfer the wort onto the Taiga Dog yeast cake.
Long before Nika and Piper died, we had planned on taking one of the dogs that Andrea’s mushing parter didn’t want, a large hound mix named Lennier (the litter was named after characters in the Babylon 5 television series). Even though we are still mourning our loss, we didn’t feel like it was a reason not to give another dog a chance in our home. He’s a yearling dog, and is a big boy, a couple inches taller than Buddy, and quite a bit longer. At the moment he is all legs, but he may still grow into his body.
Last night was a pretty taxing affair, with him too curious and excited to relax for even a minute, and a trio of cats very scared of the new resident. He has been better today, and is even sleeping on the floor at my feet right now. He appears to be mostly curious about the cats, but unfortunately, his only real experience with them so far is when they’re running away at warp speed, tails puffed.
In time, I’m sure he’ll get used to his new life, and will become part of the family. Welcome, Lennier!
Nika died today after fifteen and a half great years in our family. She was a Golden Retreiver / Australian Shepherd mix, which meant she was smart, aglie, and loved to swim. She had a beautiful, thick, dark coat that made people think she was a flat coat retriever. When she was a puppy, she needed a lot of exercise and entertainment to keep from getting bored, so she and I started a long tradition of daily (and often more) walks. I’d guess that in those fifteen years, she and I easily walked over 3,000 miles together. She loved running through the forest, swimming in every water body she came across, jumping high in the air after snow when we shovelled the deck, and when she was younger, fetching tennis balls. She came with us everywhere and was always willing to “go for a ride?!” even if it basically meant sitting in the truck once we got wherever we were going. I took her to work with me practially every day and walked her on campus, and later at the Peat Ponds.
She was a happy dog, eager to get up and go for a walk until the very end, when old age and declining strength meant she was prone to falling down and had a hard time getting up the stairs or up onto the couch. Eventually, it got to the point that we felt like she would probably rather not be around if she couldn’t do the things she loved.
I’ve spent so much time with her in the outdoors—on the trails around our property, walking up and down Goldstream Creek in the winter, hiking on campus and at the Peat Ponds at work—that I don’t know how I’m going to be able to go for a walk without missing her company. We used to sing, “Doo do da doo, Taiga Dog!” and she’d get all excited.
With the loss of Nika and Piper today, there’s a pair of huge holes in our family, and even though I know we’ll get over the pain of losing them, we will never forget them and all the happiness we shared together.

Nika post-fetch

Nika bounding

Nika on the Creek