Introduction
There are now 777 photos in my photolog, organized in reverse chronological order (or chronologically if you append /asc/ to the url). With that much data, it occurred to me that there ought to be a way to organize these photos by color, similar to the way some people organize their books. I didn’t find a way of doing that, unfortunately, but I did spend some time experimenting with image similarity analysis using color.
The basic idea is to generate histograms (counts of the pixels in the image that fit into pre-defined bins) for red, green and blue color combinations in the image. Once we have these values for each image, we use the chi square distance between the values as a distance metric that is a measure of color similarty between photos.
Code
I followed this tutorial Building your first image search engine in Python which uses code like this to generate 3D RGB histograms (all the code from this post is on GitHub):
import cv2
def get_histogram(image, bins):
""" calculate a 3d RGB histogram from an image """
if os.path.exists(image):
imgarray = cv2.imread(image)
hist = cv2.calcHist([imgarray], [0, 1, 2], None,
[bins, bins, bins],
[0, 256, 0, 256, 0, 256])
hist = cv2.normalize(hist, hist)
return hist.flatten()
else:
return None
Once you have them, you need to calculate all the pair-wise distances using a function like this:
def chi2_distance(a, b, eps=1e-10):
""" distance between two histograms (a, b) """
d = 0.5 * np.sum([((x - y) ** 2) / (x + y + eps)
for (x, y) in zip(a, b)])
return d
Getting histogram data using OpenCV in Python is pretty fast. Even with 32 bins, it only took about 45 minutes for all 777 images. Computing the distances between histograms was a lot slower, depending on how the code was written.
With 8 bin histograms, a Python script using the function listed above, took just under 15 minutes to calculate each pairwise comparison (see the rgb_histogram.py script).
Since the photos are all in a database so they can be displayed on the Internet, I figured a SQL function to calculate the distances would make the most sense. I could use the OpenCV Python code to generate histograms and add them to the database when the photo was inserted, and a SQL function to get the distances.
Here’s the function:
CREATE OR REPLACE FUNCTION chi_square_distance(a numeric[], b numeric[])
RETURNS numeric AS $_$
DECLARE
sum numeric := 0.0;
i integer;
BEGIN
FOR i IN 1 .. array_upper(a, 1)
LOOP
IF a[i]+b[i] > 0 THEN
sum = sum + (a[i]-b[i])^2 / (a[i]+b[i]);
END IF;
END LOOP;
RETURN sum/2.0;
END;
$_$
LANGUAGE plpgsql;
Unfortunately, this is incredibly slow. Instead of the 15 minutes the Python script took, it took just under two hours to compute the pairwise distances on the 8 bin histograms.
When your interpreted code is slow, the solution is often to re-write compiled code and use that. I found some C code on Stack Overflow for writing array functions. The PostgreSQL interface isn’t exactly intuitive, but here’s the gist of the code (full code):
#include <postgres.h>
#include <fmgr.h>
#include <utils/array.h>
#include <utils/lsyscache.h>
/* From intarray contrib header */
#define ARRPTR(x) ( (float8 *) ARR_DATA_PTR(x) )
PG_MODULE_MAGIC;
PG_FUNCTION_INFO_V1(chi_square_distance);
Datum chi_square_distance(PG_FUNCTION_ARGS);
Datum chi_square_distance(PG_FUNCTION_ARGS) {
ArrayType *a, *b;
float8 *da, *db;
float8 sum = 0.0;
int i, n;
da = ARRPTR(a);
db = ARRPTR(b);
// Generate the sums.
for (i = 0; i < n; i++) {
if (*da - *db) {
sum = sum + ((*da - *db) * (*da - *db) / (*da + *db));
}
da++;
db++;
}
sum = sum / 2.0;
PG_RETURN_FLOAT8(sum);
}
This takes 79 seconds to do all the distance calculates on 8 bin histograms. That kind of improvement is well worth the effort.
Results
After all that, the results aren’t as good as I was hoping. For some photos, such as the photos I took while re-raising the bridge across the creek, sorting by the histogram distances does actually identify other photos taken of the same process. For example, these two photos are the closest to each other by 32 bin histogram distance:
But there are certain images, such as the middle image in the three below that are very close to many of the photos in the database, even though they’re really not all that similar. I think this is because images with a lot of black in them (or white) wind up being similar to each other because of the large areas without color. It may be that performing the same sort of analysis using the HSV color space, but restricting the histogram to regions with high saturation and high value, would yield results that make more sense.
Yesterday I saw something I’ve never seen in a baseball game before: a runner getting hit by a batted ball, which according to Rule 7.08(f) means the runner is out and the ball is dead. It turns out that this isn’t as unusual an event as I’d thought (see below), but what was unusal is that this ended the game between the Angels and Giants. Even stranger, this is also how the game between the Diamondbacks and Dodgers ended.
Let’s use Retrosheet data to see how often this happens. Retrosheet data is organized into game data, roster data and event data. Event files contain a record of every event in a game and include the code BR for when a runner is hit by a batted ball. Here’s a SQL query to find all the matching events, who got hit and whether it was the last out in the game.
SELECT sub.game_id, teams, date, inn_ct, outs_ct, bat_team, event_tx,
first_name || ' ' || last_name AS runner,
CASE WHEN event_id = max_event_id THEN 'last out' ELSE '' END AS last_out
FROM (
SELECT year, game_id, away_team_id || ' @ ' || home_team_id AS teams,
date, inn_ct,
CASE WHEN bat_home_id = 1
THEN home_team_id
ELSE away_team_id END AS bat_team, outs_ct, event_tx,
CASE regexp_replace(event_tx, '.*([1-3])X[1-3H].*', E'\\1')
WHEN '1' THEN base1_run_id
WHEN '2' THEN base2_run_id
WHEN '3' THEN base3_run_id END AS runner_id,
event_id
FROM events
WHERE event_tx ~ 'BR'
) AS sub
INNER JOIN rosters
ON sub.year=rosters.year
AND runner_id=player_id
AND rosters.team_id = bat_team
INNER JOIN (
SELECT game_id, max(event_id) AS max_event_id
FROM events
GROUP BY game_id
) AS max_events
ON sub.game_id = max_events.game_id
ORDER BY date;
Here's what the query does. The first sub-query sub finds all the events with the BR code, determines which team was batting and finds the id for the player who was running. This is joined with the roster table so we can assign a name to the runner. Finally, it’s joined with a subquery, max_events, which finds the last event in each game. Once we’ve got all that, the SELECT statement at the very top retrieves the columns of interest, and records whether the event was the last out of the game.
Retrosheet has event data going back to 1922, but the event files don’t include every game played in a season until the mid-50s. Starting in 1955 a runner being hit by a batted ball has a game twelve times, most recently in 2010. On average, runners get hit (and are called out) about fourteen times a season.
Here are the twelve times a runner got hit to end the game, since 1955. Until yesterday, when it happened twice in one day:
| Date | Teams | Batting | Event | Runner |
|---|---|---|---|---|
| 1956-09-30 | NY1 @ PHI | PHI | S4/BR.1X2(4)# | Granny Hamner |
| 1961-09-16 | PHI @ CIN | PHI | S/BR/G4.1X2(4) | Clarence Coleman |
| 1971-08-07 | SDN @ HOU | SDN | S/BR.1X2(3) | Ed Spiezio |
| 1979-04-07 | CAL @ SEA | SEA | S/BR.1X2(4) | Larry Milbourne |
| 1979-08-15 | TOR @ OAK | TOR | S/BR.3-3;2X3(4)# | Alfredo Griffin |
| 1980-09-22 | CLE @ NYA | CLE | S/BR.3XH(5) | Toby Harrah |
| 1984-04-06 | MIL @ SEA | MIL | S/BR.1X2(4) | Robin Yount |
| 1987-06-25 | ATL @ LAN | ATL | S/L3/BR.1X2(3) | Glenn Hubbard |
| 1994-06-13 | HOU @ SFN | HOU | S/BR.1X2(4) | James Mouton |
| 2001-08-04 | NYN @ ARI | ARI | S/BR.2X3(6) | David Dellucci |
| 2003-04-09 | KCA @ DET | DET | S/BR.1X2(4) | Bobby Higginson |
| 2010-06-27 | PIT @ OAK | PIT | S/BR/G.1X2(3) | Pedro Alvarez |
And all runners hit last season:
| Date | Teams | Batting | Event | Runner |
|---|---|---|---|---|
| 2014-05-07 | SEA @ OAK | OAK | S/BR/G.1X2(3) | Derek Norris |
| 2014-05-11 | MIN @ DET | DET | S/BR/G.3-3;2X3(6);1-2 | Austin Jackson |
| 2014-05-23 | CLE @ BAL | BAL | S/BR/G.2X3(6);1-2 | Chris Davis |
| 2014-05-27 | NYA @ SLN | SLN | S/BR/G.1X2(3) | Matt Holliday |
| 2014-06-14 | CHN @ PHI | CHN | S/BR/G.1X2(4) | Justin Ruggiano |
| 2014-07-13 | OAK @ SEA | SEA | S/BR/G.1X2(4) | Kyle Seager |
| 2014-07-18 | PHI @ ATL | PHI | S/BR/G.1X2(4) | Grady Sizemore |
| 2014-07-25 | BAL @ SEA | SEA | S/BR/G.1X2(4) | Brad Miller |
| 2014-08-05 | NYN @ WAS | WAS | S/BR/G.2X3(6);3-3 | Asdrubal Cabrera |
| 2014-09-04 | SLN @ MIL | SLN | S/BR/G.2X3(6);1-2 | Matt Carpenter |
| 2014-09-09 | SDN @ LAN | LAN | S/BR/G.2X3(6) | Matt Kemp |
| 2014-09-18 | BOS @ PIT | BOS | S/BR/G.3XH(5);1-2;B-1 | Jemile Weeks |
Following up on my previous post, I tried the regression approach for predicting future snow depth from current values. As you recall, I produced a plot that showed how much snow we’ve had on the ground on each date at the Fairbanks Airport between 1917 and 2013. These boxplots gave us an idea of what a normal snow depth looks like on each date, but couldn’t really tell us much about what we might expect for snow depth for the rest of the winter.
Regression
I ran a linear regression analysis looking at how snow depth on November 8th relates to snow depth on November 27th and December 25th of the same year. Here’s the SQL:
SELECT * FROM (
SELECT extract(year from dte) AS year,
max(CASE WHEN to_char(dte, 'mm-dd') = '11-08'
THEN round(snwd_mm/25.4, 1)
ELSE NULL END) AS nov_8,
max(CASE WHEN to_char(dte, 'mm-dd') = '11-27'
THEN round(snwd_mm/25.4, 1)
ELSE NULL END) AS nov_27,
max(CASE WHEN to_char(dte, 'mm-dd') = '12-15'
THEN round(snwd_mm/25.4, 1)
ELSE NULL END) AS dec_25
FROM ghcnd_pivot
WHERE station_name = 'FAIRBANKS INTL AP'
AND snwd_mm IS NOT NULL
GROUP BY extract(year from dte)
ORDER BY year
) AS sub
WHERE nov_8 IS NOT NULL
AND nov_27 IS NOT NULL
AND dec_25 IS NOT NULL;
I’m grouping on year, then grabbing the snow depth for the three dates of interest. I would have liked to include dates in January and February in order to see how the relationship weakens as the winter progresses, but that’s a lot more complicated because then we are comparing the dates from one year to the next and the grouping I used in the query above wouldn’t work.
One note on this analysis: linear regression has a bunch of assumptions that need to be met before considering the analysis to be valid. One of these assumptions is that observations are independent from one another, which is problematic in this case because snow depth is a cumulative statistic; the depth tomorrow is necessarily related to the depth of the snow today (snow depth tomorrow = snow depth today + snowfall). Whether it’s necessarily related to the depth of the snow a month from now is less certain, and I’m making the possibly dubious assumption that autocorrelation disappears when the time interval between observations is longer than a few weeks.
Results
Here are the results comparing the snow depth on November 8th to November 27th:
> reg <- lm(data=results, nov_27 ~ nov_8)
> summary(reg)
Call:
lm(formula = nov_27 ~ nov_8, data = results)
Residuals:
Min 1Q Median 3Q Max
-8.7132 -3.0490 -0.6063 1.7258 23.8403
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.1635 0.9707 3.259 0.0016 **
nov_8 1.1107 0.1420 7.820 1.15e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.775 on 87 degrees of freedom
Multiple R-squared: 0.4128, Adjusted R-squared: 0.406
F-statistic: 61.16 on 1 and 87 DF, p-value: 1.146e-11
And between November 8th and December 25th:
> reg <- lm(data=results, dec_25 ~ nov_8)
> summary(reg)
Call:
lm(formula = dec_25 ~ nov_8, data = results)
Residuals:
Min 1Q Median 3Q Max
-10.209 -3.195 -1.195 2.781 10.791
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.2227 0.8723 7.133 2.75e-10 ***
nov_8 0.9965 0.1276 7.807 1.22e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.292 on 87 degrees of freedom
Multiple R-squared: 0.412, Adjusted R-squared: 0.4052
F-statistic: 60.95 on 1 and 87 DF, p-value: 1.219e-11
Both regressions are very similar. The coefficients and the overall model are both very significant, and the R² value indicates that in each case, the snow depth on November 8th explains about 40% of the variation in the snow depth on the later date. The amount of variation explained hardly changes at all, despite almost a month difference between the two analyses.
Here's a plot of the relationship between today’s date and Christmas (PDF version)
The blue line is the linear regression model.
Conclusions
For 2014, we’ve got 2 inches of snow on the ground on November 8th. The models predict we’ll have 5.4 inches on November 27th and 8 inches on December 25th. That isn’t great, but keep in mind that even though the relationship is quite strong, it explains less than half of the variation in the data, which means that it’s quite possible we will have a lot more, or less. Looking back at the plot, you can see that for all the years where we had two inches of snow on November 8th, we had between five and fifteen inches of snow in that same year on December 25th. I’m certainly hoping we’re closer to fifteen.
Winter started off very early this year with the first snow falling on October 4th and 5th, setting a two inch base several weeks earlier than normal. Since then, we’ve had only two days with more than a trace of snow.
This seems to be a common pattern in Fairbanks. After the first snowfall and the establishment of a thin snowpack on the ground, we all get excited for winter and expect the early snow to continue to build, filling the holes in the trails and starting the skiing, mushing and winter fat biking season. Then, nothing.
Analysis
I decided to take a quick look at the pattern of snow depth at the Fairbanks Airport station to see how uncommon it is to only have two inches of snow this late in the winter (November 8th at this writing). The plot below shows all of the snow depth data between November and April for the airport station, displayed as box and whisker plots.
Here’s the SQL:
SELECT extract(year from dte) AS year,
extract(month from dte) AS month,
to_char(dte, 'MM-DD') AS mmdd,
round(snwd_mm/25.4, 1) AS inches
FROM ghcnd_pivot
WHERE station_name = 'FAIRBANKS INTL AP'
AND snwd_mm IS NOT NULL
AND (extract(month from dte) BETWEEN 11 AND 12
OR extract(month from dte) BETWEEN 1 AND 4);
If you’re interested in the code that produces the plot, it’s at the bottom of the post. If the plot doesn’t show up in your browser or you want a copy for printing, here’s a link to the PDF version.
Box and whisker plots
For those unfamiliar with these, they’re a good way to evaluate the range of data grouped by some categorical variable (date, in our case) along with details about the expected values and possible extremes. The upper and lower limit of each box show the ranges where 25—75% of the data fall, meaning that half of all observed values are within this box for each date. For example, on today’s date, November 8th, half of all snow depth values for the period in question fell between four and eight inches. Our current snow depth of two inches falls below this range, so we can say that only having two inches of snow on the ground happens in less than 25% of the time.
The horizontal line near the middle of the box is the median of all observations for that date. Median is shown instead of average / mean because extreme values can skew the mean, so a median will often be more representative of the most likely value. For today’s date, the median snow depth is five inches. That’s what we’d expect to see on the ground now.
The vertical lines extending above and below the boxes show the points that are within 1.5 times the range of the boxes. These lines represent the values from the data outside the most likely, but not very unusual. If you scan across the November to December portion of the plot, you can see that the lower whisker touches zero for most of the period, but starting on December 26th, it rises above zero and doesn’t return until the spring. That means that there have been years where there was no snow on the ground on Christmas. Ouch.
The dots beyond the whiskers are outliers; observations so far from what is normal that they’re exceptional and not likely to be repeated. On this plot, most of these outliers are probably from one or two exceptional years where we got a ton of snow. Some of those outliers are pretty incredible; consider having two and a half feet of snow on the ground at the end of April, for example.
Conclusion
The conclusion I’d draw from comparing our current snow depth of two inches against the boxplots is that it is somewhat unusual to have this little snow on the ground, but that it’s not exceptional. It wouldn’t be unusual to have no snow on the ground.
Looking forward, we would normally expect to have a foot of snow on the ground by mid-December, and I’m certainly hoping that happens this year. But despite the probabilities shown on this plot it can’t say how likely that is when we know that there’s only two inches on the ground now. One downside to boxplots in an analysis like this is that the independent variable (date) is categorical, and the plot doesn’t have anything to say about how the values on one day relate to the values on the next day or any date in the future. One might expect, for example, that a low snow depth on November 8th means it’s more likely we’ll also have a low snow depth on December 25th, but this data can’t offer evidence on that question. It only shows us what each day’s pattern of snow depth is expected to be on it’s own.
Bayesian analysis, “given a snow depth of two inches on November 8th, what is the likelihood of normal snow depth on December 25th”, might be a good approach for further investigation. Or a more traditional regression analysis examining the relationship between snow depth on one date against snow depth on another.
Appendix: R Code
library(RPostgreSQL)
library(ggplot2)
library(scales)
library(gtable)
# Build plot "table"
make_gt <- function(nd, jf, ma) {
gt1 <- ggplot_gtable(ggplot_build(nd))
gt2 <- ggplot_gtable(ggplot_build(jf))
gt3 <- ggplot_gtable(ggplot_build(ma))
max_width <- unit.pmax(gt1$widths[2:3], gt2$widths[2:3], gt3$widths[2:3])
gt1$widths[2:3] <- max_width
gt2$widths[2:3] <- max_width
gt3$widths[2:3] <- max_width
gt <- gtable(widths = unit(c(11), "in"), heights = unit(c(3, 3, 3), "in"))
gt <- gtable_add_grob(gt, gt1, 1, 1)
gt <- gtable_add_grob(gt, gt2, 2, 1)
gt <- gtable_add_grob(gt, gt3, 3, 1)
gt
}
drv <- dbDriver("PostgreSQL")
con <- dbConnect(drv, dbname="DBNAME")
results <- dbGetQuery(con,
"SELECT extract(year from dte) AS year,
extract(month from dte) AS month,
to_char(dte, 'MM-DD') AS mmdd,
round(snwd_mm/25.4, 1) AS inches
FROM ghcnd_pivot
WHERE station_name = 'FAIRBANKS INTL AP'
AND snwd_mm IS NOT NULL
AND (extract(month from dte) BETWEEN 11 AND 12
OR extract(month from dte) BETWEEN 1 AND 4);")
results$mmdd <- as.factor(results$mmdd)
# NOV DEC
nd <- ggplot(data=subset(results, month == 11 | month == 12), aes(x=mmdd, y=inches)) +
geom_boxplot() +
theme_bw() +
theme(axis.title.x = element_blank()) +
theme(plot.margin = unit(c(1, 1, 0, 0.5), 'lines')) +
# scale_x_discrete(name="Date (mm-dd)") +
scale_y_discrete(name="Snow depth (inches)", breaks=pretty_breaks(n=10)) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
ggtitle('Snow depth by date, Fairbanks Airport, 1917-2013')
# JAN FEB
jf <- ggplot(data=subset(results, month == 1 | month == 2), aes(x=mmdd, y=inches)) +
geom_boxplot() +
theme_bw() +
theme(axis.title.x = element_blank()) +
theme(plot.margin = unit(c(0, 1, 0, 0.5), 'lines')) +
# scale_x_discrete(name="Date (mm-dd)") +
scale_y_discrete(name="Snow depth (inches)", breaks=pretty_breaks(n=10)) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) # +
# ggtitle('Snowdepth by date, Fairbanks Airport, 1917-2013')
# MAR APR
ma <- ggplot(data=subset(results, month == 3 | month == 4), aes(x=mmdd, y=inches)) +
geom_boxplot() +
theme_bw() +
theme(plot.margin = unit(c(0, 1, 1, 0.5), 'lines')) +
scale_x_discrete(name="Date (mm-dd)") +
scale_y_discrete(name="Snow depth (inches)", breaks=pretty_breaks(n=10)) +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) # +
# ggtitle('Snowdepth by date, Fairbanks Airport, 1917-2013')
gt <- make_gt(nd, jf, ma)
svg("snowdepth_boxplots.svg", width=11, height=9)
grid.newpage()
grid.draw(gt)
dev.off()
I’m writing this blog post on May 1st, looking outside as the snow continues to fall. We’ve gotten three inches in the last day and a half, and I even skied to work yesterday. It’s still winter here in Fairbanks.
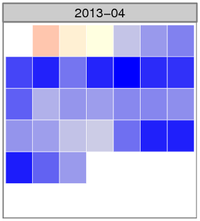
The image shows the normalized temperature anomaly calendar heatmap for April. The bluer the squares are, the colder that day was compared with the 30-year climate normal daily temperature for Fairbanks. There were several days where the temperature was more than three standard deviations colder than the mean anomaly (zero), something that happens very infrequently.
Here are the top ten coldest average April temperatures for the Fairbanks Airport Station.
| Rank | Year | Average temp (°F) | Rank | Year | Average temp (°F) |
|---|---|---|---|---|---|
| 1 | 1924 | 14.8 | 6 | 1972 | 20.8 |
| 2 | 1911 | 17.4 | 7 | 1955 | 21.6 |
| 3 | 2013 | 18.2 | 8 | 1910 | 22.9 |
| 4 | 1927 | 19.5 | 9 | 1948 | 23.2 |
| 5 | 1985 | 20.7 | 10 | 2002 | 23.2 |
The averages come from the Global Historical Climate Network - Daily data set, with some fairly dubious additions to extend the Fairbanks record back before the 1956 start of the current station. Here’s the query to get the historical data:
SELECT rank() OVER (ORDER BY tavg) AS rank,
year, round(c_to_f(tavg), 1) AS tavg
FROM (
SELECT year, avg(tavg) AS tavg
FROM (
SELECT extract(year from dte) AS year,
dte, (tmin + tmax) / 2.0 AS tavg
FROM (
SELECT dte,
sum(CASE WHEN variable = 'TMIN'
THEN raw_value * 0.1
ELSE 0 END) AS tmin,
sum(CASE WHEN variable = 'TMAX'
THEN raw_value * 0.1
ELSE 0 END) AS tmax
FROM ghcnd_obs
WHERE variable IN ('TMIN', 'TMAX')
AND station_id = 'USW00026411'
AND extract(month from dte) = 4 GROUP BY dte
) AS foo
) AS bar GROUP BY year
) AS foobie
ORDER BY rank;
And the way I calculated the average temperature for this April. pafg is a text file that includes the data from each day’s National Weather Service Daily Climate Summary. Average daily temperature is in column 9.
$ tail -n 30 pafg | \
awk 'BEGIN {sum = 0; n = 0}; {n = n + 1; sum += $9} END { print sum / n; }'
18.1667