Next month I’ll be attending a game at Wrigley Field and my brother and I had some discussion about the best strategy for us to meet up somewhere in Chicago after the game. Knowing how long a game could be, and how many people are likely to be crowding the train platforms is useful information that can be inferred from the game data that http://www.retrosheet.org/ collects and distributes.
It’s also a good excuse to fiddle around the the IPython Notebook, pandas and the rest of the Python scientific computing stack.
I downloaded the game log data from http://www.retrosheet.org/gamelogs/index.html using this bash one-liner:
for i in `seq 1871 2012`; \
do wget http://www.retrosheet.org/gamelogs/gl${i}.zip ; \
unzip gl${i}.zip; \
rm gl${i}.zip; \
done
Game Length
Game length in minutes is in column 19. Let’s read it and analyze it with Pandas.
import pandas as pd
import matplotlib.pyplot as plt
import datetime
def fix_df(input_df, cols):
""" Pulls out the columns from cols, labels them and returns
a new DataFrame """
df = pd.DataFrame(index=range(len(input_df)))
for k, v in cols.items():
df[v] = input_df[k]
return df
cols = {0:'dt_str', 2:'day_of_week', 3:'visiting_team',
6:'home_team', 9:'visitor_score', 10:'home_score',
11:'game_outs', 12:'day_night', 13:'complete',
16:'park_id', 17:'attendance', 18:'game_time_min'}
raw_gamelogs = []
for i in range(1871, 2013):
fn = "GL{0}.TXT".format(i)
raw_gamelogs.append(pd.read_csv(fn, header=None, index_col=None))
raw_gamelog = pd.concat(raw_gamelogs, ignore_index=True)
gamelog = fix_df(raw_gamelog, cols)
gamelog['dte'] = gamelog.apply(
lambda x: datetime.datetime.strptime(str(x['dt_str']), '%Y%m%d').date(),
axis=1)
gamelog.ix[0:5, 1:] # .head() but without the dt_str col
| dow | vis | hme | vis | hme | outs | day | park | att | time | dte | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Thu | CL1 | FW1 | 0 | 2 | 54 | D | FOR01 | 200 | 120 | 1871-05-04 |
| 1 | Fri | BS1 | WS3 | 20 | 18 | 54 | D | WAS01 | 5000 | 145 | 1871-05-05 |
| 2 | Sat | CL1 | RC1 | 12 | 4 | 54 | D | RCK01 | 1000 | 140 | 1871-05-06 |
| 3 | Mon | CL1 | CH1 | 12 | 14 | 54 | D | CHI01 | 5000 | 150 | 1871-05-08 |
| 4 | Tue | BS1 | TRO | 9 | 5 | 54 | D | TRO01 | 3250 | 145 | 1871-05-09 |
| 5 | Thu | CH1 | CL1 | 18 | 10 | 48 | D | CLE01 | 2500 | 120 | 1871-05-11 |
(Note that I’ve abbreviated the column names so they fit)
The data looks reasonable, although I don’t know quite what to make of the team names from back in 1871. Now I’ll take a look at the game time data for the whole data set:
times = gamelog['game_time_min']
times.describe()
count 162259.000000 mean 153.886145 std 74.850459 min 21.000000 25% 131.000000 50% 152.000000 75% 173.000000 max 16000.000000
The statistics look reasonable, except that it’s unlikley that there was a completed game in 21 minutes, or that a game took 11 days, so we have some outliers in the data. Let’s see if something else in the data might help us filter out these records.
First the games longer than 24 hours:
print(gamelog[gamelog.game_time_min > 60 * 24][['visiting_team',
'home_team', 'game_outs', 'game_time_min']])
print("Removing all NaN game_outs: {0}".format(
len(gamelog[np.isnan(gamelog.game_outs)])))
print("Max date removed: {0}".format(
max(gamelog[np.isnan(gamelog.game_outs)].dte)))
visiting_team home_team game_outs game_time_min
26664 PHA WS1 NaN 12963
26679 PHA WS1 NaN 4137
26685 WS1 PHA NaN 16000
26707 NYA PHA NaN 15115
26716 CLE CHA NaN 3478
26717 DET SLA NaN 1800
26787 PHA NYA NaN 3000
26801 PHA NYA NaN 6000
26880 CHA WS1 NaN 2528
26914 SLA WS1 NaN 2245
26921 SLA WS1 NaN 1845
26929 CLE WS1 NaN 3215
Removing all NaN game_outs: 37890
Max date removed: 1915-10-03
There’s no value for game_outs, so there isn’t data for how long the game actually was. We remove 37,890 records by eliminating this data, but these are all games from prior to the 1916 season, so it seems reasonable:
gamelog = gamelog[pd.notnull(gamelog.game_outs)]
gamelog.game_time_min.describe()
count 156639.000000 mean 154.808975 std 32.534916 min 21.000000 25% 133.000000 50% 154.000000 75% 174.000000 max 1150.000000
What about the really short games?
gamelog[gamelog.game_time_min < 60][[
'dte', 'game_time_min', 'game_outs']].tail()
dte game_time_min game_outs
79976 1948-07-02 24 54
80138 1948-07-22 59 30
80982 1949-05-29 21 42
113455 1971-07-30 48 27
123502 1976-09-10 57 30
Many of these aren’t nine inning games because there are less than 51 outs (8 innings for a home team, 9 for the visitor in a home team win ✕ 3 innings = 51). At the moment, I’m interested in looking at how long a game is likely to be, rather than the pattern of game length over time, so we can leave these records in the data.
Now we filter the data to just the games played since 2000.
twenty_first = gamelog[gamelog['dte'] > datetime.date(1999, 12, 31)]
times_21 = twenty_first['game_time_min']
times_21.describe()
count 31580.000000 mean 175.084421 std 26.621124 min 79.000000 25% 157.000000 50% 172.000000 75% 189.000000 max 413.000000
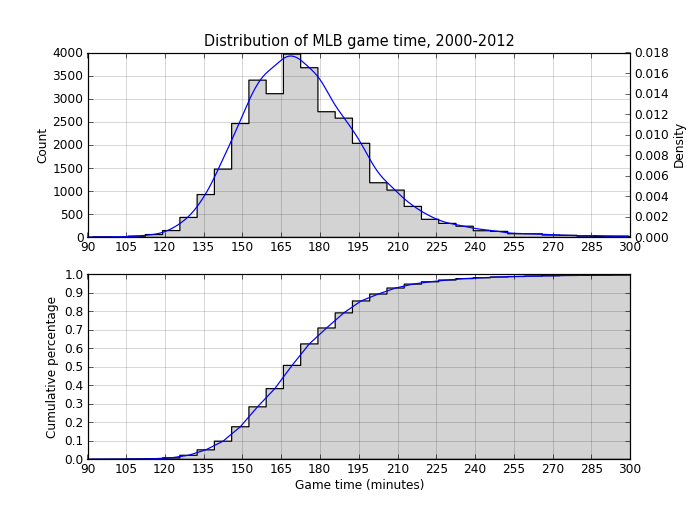
The average game length between 2000 and 2012 is 175 minutes, or just under three hours. And three quarters of all the games played are under three hours and ten minutes.
Here’s the code to look at the distribution of these times. The top plot shows a histogram (the count of the games in each bin) and a density estimation of the same data.
The second plot is a cumulative density plot, which makes it easier to see what percentage of games are played within a certain time.
from scipy import stats
# Calculate a kernel density function
density = stats.kde.gaussian_kde(times_21)
x = range(90, 300)
rc('grid', linestyle='-', alpha=0.25)
fig, axes = plt.subplots(ncols=1, nrows=2, figsize=(8, 6))
# First plot (histogram / density)
ax = axes[0]
ax2 = ax.twinx()
h = ax.hist(times_21, bins=50, facecolor="lightgrey", histtype="stepfilled")
d = ax2.plot(x, density(x))
ax2.set_ylabel("Density")
ax.set_ylabel("Count")
plt.title("Distribution of MLB game times, 2000-2012")
ax.grid(True)
ax.set_xlim(90, 300)
ax.set_xticks(range(90, 301, 15))
# Second plot (cumulative histogram)
ax1 = axes[1]
n, bins, patches = ax1.hist(times_21, bins=50, normed=True, cumulative=True,
facecolor="lightgrey", histtype="stepfilled")
y = n / float(n[-1]) # Convert counts to percentage of total
y = np.concatenate(([0], y))
bins = bins - ((bins[1] - bins[0]) / 2.0) # Center curve on bars
ax1.plot(bins, y, color="blue")
ax1.set_ylabel("Cumulative percentage")
ax1.set_xlabel("Game time (minutes)")
ax1.grid(True)
ax1.set_xlim(90, 300)
ax1.set_xticks(range(90, 301, 15))
ax1.set_yticks(np.array(range(0, 101, 10)) / 100.0)
plt.savefig('game_time.png', dpi=87.5)
plt.savefig('game_time.svg')
plt.savefig('game_time.pdf')
The two plots show what the descriptive statistics did: 70% of games are under three hours but it’s not uncommon for games to last three hours and fifteen minutes. Beyond that, it’s pretty uncommon.
Change in game times in the last 100 years
Now let’s look at how game times have changed over the years. First we eliminate all the games that weren’t complete in 51 or 54 innings to standardize the “game” were’re evaluating.
nine_innings = gamelog[gamelog.game_outs.isin([51, 54])]
nine_innings['year'] = nine_innings.apply(lambda x: x['dte'].year, axis=1)
nine_groupby_year = nine_innings.groupby('year')
mean_time_by_year = nine_groupby_year['game_time_min'].aggregate(np.mean)
fig = plt.figure()
p = mean_time_by_year.plot(figsize=(8, 4))
p.set_xlim(1915, 2015)
p.set_xlabel('Year')
p.set_ylabel('Game Time (minutes)')
p.set_title('Average MLB nine-inning game time since 1915')
p.set_xticks(range(1915, 2016, 10))
plt.savefig('game_time_by_year.png', dpi=87.5)
plt.savefig('game_time_by_year.svg')
plt.savefig('game_time_by_year.pdf')
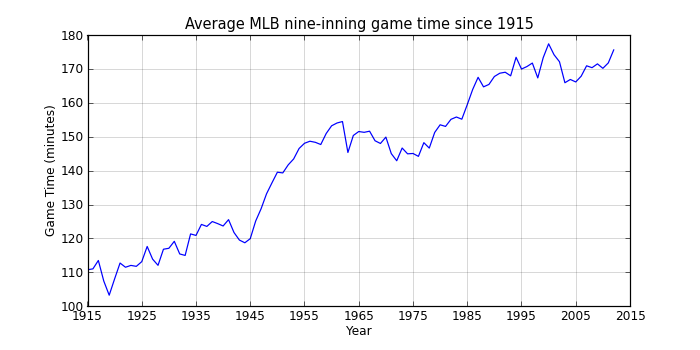
That shows a pretty clear upward trend interrupted by a slight decline between 1960 and 1975 (when offense was down across baseball). Since the mid-90s, game times have hovered around 2:50, so maybe MLB’s efforts at increasing the pace of the game have at least stopped what had been an almost continual rise in game times.
Attendance
I’ll be seeing a game at Wrigley Field, so let’s examine attendance at Wrigley.
Attendance is field 17, “Park ID” is field 16, but we can probably use Home team (field 6) = “CHN” for seasons after 1914 when it opened.
twenty_first[twenty_first['home_team'] == 'CHN']['attendance'].describe()
count 1053.000000 mean 37326.561254 std 5544.121773 min 0.000000 25% 36797.000000 50% 38938.000000 75% 40163.000000 max 55000.000000
We see the minimum is zero, which may indicate bad or missing data. Let’s look at all the games at Wrigley with less than 10,000 fans:
twenty_first[(twenty_first.home_team == 'CHN') &
(twenty_first.attendance < 10000)][[
'dte', 'visiting_team', 'home_team', 'visitor_score',
'home_score', 'game_outs', 'day_night', 'attendance',
'game_time_min']]
| dte | vis | hme | vis | hme | outs | day | att | game_time | |
|---|---|---|---|---|---|---|---|---|---|
| 172776 | 2000-06-01 | ATL | CHN | 3 | 5 | 51 | D | 5267 | 160 |
| 173897 | 2000-08-25 | LAN | CHN | 5 | 3 | 54 | D | 0 | 189 |
| 174645 | 2001-04-18 | PHI | CHN | 3 | 4 | 51 | D | 0 | 159 |
| 176290 | 2001-08-20 | MIL | CHN | 4 | 7 | 51 | D | 0 | 180 |
| 177218 | 2002-04-28 | LAN | CHN | 5 | 4 | 54 | D | 0 | 196 |
| 177521 | 2002-05-21 | PIT | CHN | 12 | 1 | 54 | N | 0 | 158 |
| 178910 | 2002-09-02 | MIL | CHN | 4 | 2 | 54 | D | 0 | 193 |
| 181695 | 2003-09-27 | PIT | CHN | 2 | 4 | 51 | D | 0 | 169 |
| 183806 | 2004-09-10 | FLO | CHN | 7 | 0 | 54 | D | 0 | 146 |
| 184265 | 2005-04-13 | SDN | CHN | 8 | 3 | 54 | D | 0 | 148 |
| 188186 | 2006-08-03 | ARI | CHN | 10 | 2 | 54 | D | 0 | 197 |
Looks like the zeros are just missing data because these games have relevant data for the other fields and it’s impossible to believe that not a single person was in the stands. We’ll get rid of them for the attendance analysis.
Now we’ll filter the games so we’re only looking at day games played at Wrigley where the attendance value is above zero, and group the data by day of the week.
groupby_dow = twenty_first[(twenty_first['home_team'] == 'CHN') &
(twenty_first['day_night'] == 'D') &
(twenty_first['attendance'] > 0)].groupby('day_of_week')
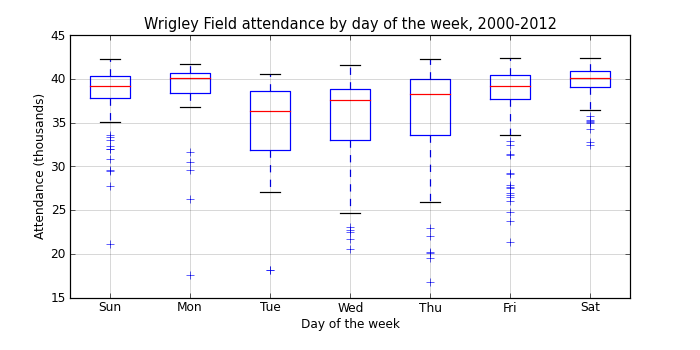
groupby_dow['attendance'].aggregate(np.mean).order()
day_of_week Tue 34492.428571 Wed 35312.265957 Thu 35684.737864 Mon 37938.757576 Fri 38066.060976 Sun 38583.833333 Sat 39737.428571 Name: attendance
And plot it:
filtered = twenty_first[(twenty_first['home_team'] == 'CHN') &
(twenty_first['day_night'] == 'D') &
(twenty_first['attendance'] > 0)]
dows = {'Sun':0, 'Mon':1, 'Tue':2, 'Wed':3, 'Thu':4, 'Fri':5, 'Sat':6}
filtered['dow'] = filtered.apply(lambda x: dows[x['day_of_week']], axis=1)
filtered['attendance'] = filtered['attendance'] / 1000.0
fig = plt.figure()
d = filtered.boxplot(column='attendance', by='dow', figsize=(8, 4))
plt.suptitle('')
d.set_xlabel('Day of the week')
d.set_ylabel('Attendance (thousands)')
d.set_title('Wrigley Field attendance by day of the week, 2000-2012')
labels = ['Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
l = d.set_xticklabels(labels)
d.set_ylim(15, 45)
plt.savefig('attendance.png', dpi=87.5)
plt.savefig('attendance.svg') # lines don't show up?
plt.savefig('attendance.pdf')
There’s a pretty clear pattern here, with increasing attendance from Tuesday through Monday, and larger variances in attendance during the week.
It’s a bit surprising that Monday games are as popular as Saturday games, especially since we’re only looking at day games. On any given Monday when the Cubs are at home, there’s a good chance that there will be fourty thousand people not showing up to work!